テクニカル指標にフィボナッチ数を使うものはいろいろあるようですが、多くの場合、「フィボナッチライン」というと「フィボナッチ・リトレースメント」を指します。
ということでここでは
フィボナッチライン=フィボナッチ・リトレースメント
として話を進めていきます。
フィボナッチラインはツールで簡単に引ける
そのフィボナッチラインを株やFXのトレードに使う方法ですが・・・これは単純です。
証券会社のチャートツールに、フィボナッチ・リトレースメントっていうのがあると思いますので、それでラインを引くだけです。
SBIであればハイパーSBIで簡単に引くことができます。
で、その引き方ですけど・・・上がったり下がったりしているチャートがありますよね。
その、上がったり下がったりの、頂上が100、谷底が0になるようにフィボナッチラインを引くだけです。
あ、別に0と100は逆でもいいです。
そうすると、フィボナッチ数に基づいたその他のライン、23.6、38.2、50、61.8、76.4も自動的に引かれるはずです。
どこの頂上と谷底を選ぶのか
じゃあどこを「頂上」「谷底」として選ぶのかというと、それはトレードの時間軸によって異なります。
長期で考えている人は、すご~く昔の頂上や谷底と現在の頂上や谷底を結ぶでしょうし、短期で考えている人は直近のものを重視するでしょう。
まあ短期であっても長期的な節目は気にするものですので、そこは必要に応じて何種類か引くことになります。
長期目線のフィボナッチと、短期目線のフィボナッチ。
さて。
フィボナッチラインの活用法
ラインを引いたあとの利用法ですが、これも単純です。
フィボナッチラインを、サポートライン、レジストラインとして活用します。
「ここで反転するかな」とか「ブレイクするかな」とか、そういう目で見て、エントリーの参考にするということです。
もちろんその場合は、出来高も同時に確認して「動きの意図」も想像します。出来高を伴っていれば「ああ、そっちに行きたいんだな」と推測するということ。
以上がフィボナッチラインの簡単な使い方です。
で。
フィボナッチラインの根拠
思いますよね?
「フィボナッチになんの根拠があるの?」
と。
端的に言ってしまえば「心理的なもの」です。
人間が「これくらいがちょうどいいんじゃない?」と思う割合というわけ。
そしてそれを最近は、機関などがAIでトレードしたりするものだから、AIのアルゴリズムにも取り入れられていると考えられます。
多くのAIが取り入れていれば・・・AIに心理なんてありませんから、プログラムされたとおり、フィボナッチラインで反応することになります。
でもあの・・・なんで人間が「これくらいがちょうどいいんじゃない?」って思うのか、気になりますよね。
まずこれ、「数学的に美しいから」ということが考えられます。
もう一つは「自然界に多く見られるから」ということもあるでしょう。
フィボナッチ数とは
フィボナッチ数というのは何かというと・・・昔々の数学者レオナルド・フィボナッチさんが、自らの研究と言うか趣味というか、その中で見出した数字なんです。
だからフィボナッチさんの名前を取って「フィボナッチ数」と呼ばれます。
どういう数字かというと・・・こういう数字です。
0,1,1,2,3,5,8,13,21・・・
これがフィボナッチ数。このまま規則的に続いていくのでまとめて「フィボナッチ数列」と呼びます。
なんか・・・よくありそうですよね。数学の問題とかで。
「この数列の、21の次に来る数字はなんですか?」
とか。^^;
なんでしょう?^^;^^;
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
考え中
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
はい。
正解は「34」です。^^
これ、フィボナッチ数について全く知らずにわかった人、すごいです。^^
それでこの・・・
0,1,1,2,3,5,8,13,21・・・
フィボナッチ数に、どんな規則があるのかと。
前の2つの数字を足す、それだけ。
最初の0と1は固定です。最初の2つの数字はこれと決めてしまいました。フィボナッチさんが。
でもこの最初の2つを決めるだけで、後に続く数列が全部決まってしまいます。
どう決まるのかというと・・・「前の2つの数字を足す」これだけ。
つまり最初の0と1の次は、「0+1」で1ですね。
0,1,1,2,3,5,8,13,21・・・
その次は「1+1=2」、その次は「1+2=3」、以降「2+3=5」「3+5=8」・・・と続いていきます。
これがフィボナッチ数列です。
で?
それがどうした。
ということになりそうですが、この数列に
「黄金比」
が隠されているのが面白いところ。
フィボナッチ数列に隠されている黄金比
黄金比ってあれです。
1:1.618
というやつ。
モナリザとかパルテノン神殿とか、日本では金閣なんかにも取り入れられている数字。
「人間にとって美しく見える」ものはだいたいこの黄金比に近くなっています。
「え? フィボナッチ数のどこから1.618って出て来るの?」
って思いますよね・・・
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597・・・
これ、あとの数字を前の数字で割ると、だんだん「1.618」に近づいていきます。
1÷1=1
2÷1=2
3÷2=1.5
5÷3=1.66…
8÷5=1.6
13÷8=1.625
(間省略^^;)
1597÷987=1.618…
というように。
ちなみに、これを逆に割り算すると「0.618」に近づいていきます。
987÷1597=0.618…
で。
人間が見て「美しい」と思える比率
この黄金比ですが、人間が作った美術品や建築物だけでなく、自然の中にも出てくるのが面白いところです。
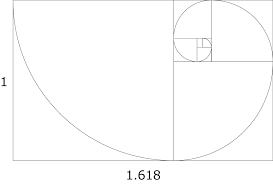
たとえば、黄金比に基づいてこのような螺旋がかけますが・・・
こういう螺旋は、植物とか、巻き貝とか、大きなところでは台風とか、銀河とか^^;
そういうところで見られます。
自然の中に見られる安定した比率だから、人間から見て「ちょうどいいな」と思えるのでしょうね。
だからそれが人工的な美術品や建築物にも取り入れられたと。
ただその数字が、フィボナッチ数列の中に隠されているというのは神秘的です。
だって、フィボナッチ数列というのは、自然を観察して帰納的に導かれたものではなく、単に前の数字を足していっているだけですからね?
そこに黄金比が隠されているなんて・・・神様のちょっとした遊び心でしょうか。^^
それはさておき。
フィボナッチラインに話を戻しましょう。
ちょっと待って、フィボナッチのその他の数字は?
フィボナッチラインは谷底と頂上、二つのポイントを0と100に設定すると、それ以外のラインが自動で引かれるものでしたね。
100
76.4
61.8
50
38.2
23.6
0
この割合でラインが引かれます。
このうち「61.8」というのは上述した「黄金比」の数字ですね。「38.2」はその反対側です。つまり「100-61.8」ですね。
ちなみに、38.2%、つまり0.382という数字もフィボナッチ数列から計算できます。
一つ後の数字で割ると0.618なんですが、2つ後の数字で割ると0.382となります。
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597・・・
これから、
610÷1597=0.3819…
じゃあフィボナッチラインの23.6%と76.4%は?
23.6は3つ後の数字で割ると出てきます。
377÷1597=0.236…
76.4%はその反対側ですね。「100-23.6」です。
で。
100
76.4
61.8
50
38.2
23.6
0
「50」って何?
と思いますけど、まあこれは「ちょうど半分」というのも人間にとってキリがいいから、ということなんでしょう。
チャートの動きで「半値押し」「半値戻し」ってよくありますから。